ЗАРОЖДЕНИЕ НОВОЙ ФАЗЫ (зародышеобразование, нуклеация), процесс флуктуационного образования жизнеспособных центров выделения новой фазы при фазовых переходах первого рода. Различают 3. н. ф. гомогенное (в объеме материнской фазы) и гетерогенное (на посторонних частицах, пов-стях сосудов и др.). Закономерности 3. н. ф. и послед. роста зародышей при кристаллизации, конденсации пара, кипении и расслаивании р-ров определяют строение образующихся дисперсных систем и должны учитываться при анализе условий протекания этих процессов в природе и технике.
3. н. ф., как правило, происходит при метастабильном состоянии исходной системы.
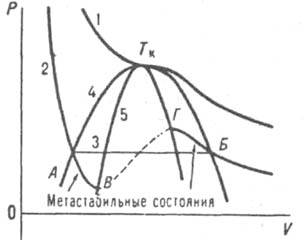
Рис. 1. Зависимости давления от объема при критич. т-ре (1) и ниже критич. т-ры (2); пунктирная часть кривой 2 отвечает лабильным состояниям; прямая 3 соединяет равновесные состояния жидкости и пара; 4 - бинодаль; 5 -спинодаль; Тк - критич. точка.
При конденсации пара (рис. 1)
область метастабильного состояния на диаграмме давление р - объем V расположена между бинодалью, т. е. кривой, соединяющей точки, отвечающие равновесным состояниям при разных т-рах Т для жидкости и пара (соотв. точки А и Б), и спинодалью - кривой, соединяющей точки, в к-рых dp/dV=0 (точки В и Г). Под спинодалью расположена область абс. неустойчивости системы (область лабильных состояний). Степень отклонения системы от равновесного состояния, или глубина ее внедрения в метастабильную область, характеризуется разностью хим. потенциалов Dm между метастабильной исходной фазой (И. ф.) и стабильной новой фазой (Н. ф.): Dm = mИ. ф. — mН.ф. Величина Dm м. б. выражена через непосредственно измеримые величины с использованием обычных термодинамич. соотношений (далее приводятся простейшие выражения, к-рые м. б. уточнены с помощью обычных термодинамич. приемов, напр., введением коэф. активности):
- при конденсации пара, давление к-рого р: Dm = RTln(p/p0) где р0 - давление насыщ. пара, R - универсальная газовая постоянная. Т - абс. т-ра. р/р0 - пересыщенис пара;
- при кристаллизации однокомпонентных частиц из р-ра концентрации с: Dm = RTln(с/с0), где с0 - р-римость при т-ре кристаллизации, с/с0 - пересышение р-ра;
- при кристаллизации расплава при т-ре Т, более низкой, чем т-ра плавления T0: Dm = DНпл.DT/T0, где DНпл - теплота плавления, DT= T0 — Т - переохлаждение расплава;
- при кипении при т-ре Т, более высокой, чем т-ра кипения Т0, или давлении р, более низком, чем давление насыщ. пара р0: Dm = DНисп.DT/T0 = Vm (р0 - р), где DT = Т - T0 -
перегрев жидкости, Vm - ее молярный объем (Vm = M/d; М - мол. масса, d - плотность жидкости); давление р м. б. и отрицательным (для т. н. растянутых жидкостей, напр., в пузырьковых камерах, применяемых для регистрации элементарных частиц).
Термодинамическая теория З. н. ф., развитая Дж. Гиббсом (1876-78) и М. Фольмером (1939), учитывает уменьшение энергии системы при образовании зародыша вследствие перехода в-ва в термодинамически более стабильное состояние и рост энергии, связанный с образованием пов-сти раздела И. ф. - Н. ф. При гомогенном образовании сферич. зародыша радиуса r (капля, пузырьки) при постоянных давлении и т-ре изменение своб. энергии Гиббса DG равно:
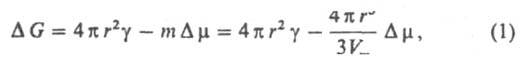
здесь g - поверхностное натяжение (уд. свободная поверхностная энергия), т - кол-во в-ва Н. ф. в частице (в молях), Vт - его молярный объем. Зависимость DG(r) имеет максимум при r = rк (рис. 2), к-рому отвечает состояние неустойчивого равновесия между зародышем и И. ф.
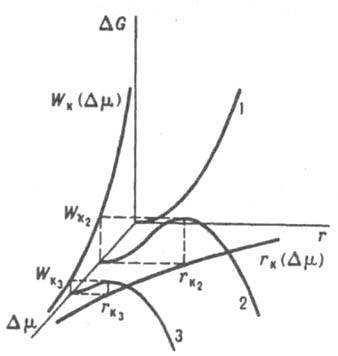
Рис. 2. Влияние глубины внедрения в метастабильную область Dm на зависимость изменения термодинамич. потенциала Гиббса DG от радиуса зародыша новой фазы r, радиус критич. зародыша rк и работу его образования Wк. Кривая 1 - Dm = 0, кривые 2 и 3 отвечают возрастающим значениям Dm.
В этом состоянии хим. потенциал в-ва Н. ф. в зародыше, повышенный за счет действия капиллярного давления Dрg = 2g/r, равен его хим. потенциалу в И. ф. В частицах с размером, меньшим rк, хим. потенциал в-ва выше, чем в И. ф., и они стремятся уменьшить свой размер. Частицы, у к-рых r больше rк, имеют более низкий хим. потенциал и могут неограниченно расти за счет перехода в-ва в них из материнской фазы. Частица с радиусом rк наз. поэтому критич. зародышем; rк = 2gVm/Dm. Для его возникновения необходимо затратить работу Wк, равную (по Гиббсу) одной трети его поверхностной энергии:
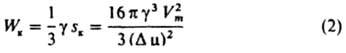
(sк - пов-сть критич. зародыша). Величину Wк можно рассматривать как высоту энергетич. барьера при З. н. ф.; его преодоление осуществляется флуктуационным путем (см. ниже). Чем больше глубина внедрения в метастабильную область (Dm), тем ниже высота энергетич. барьера Wк.
Работа образования критич. зародыша может уменьшаться при гетерог. З. н. ф., напр., при образовании зародыша на смачиваемой им пов-сти (рис. 3); при этом радиус кривизны пов-сти критич. зародыша rк остается неизменным, а соотношение работ гетерог. Wкгет и гомог Wкгом образований критич. зародышей равно отношению их объемов.
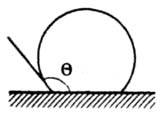
Рис. 3. Гетерогенное образование зародыша на плоской пов-сти (Q - краевой угол избират. смачивания)
При возникновении зародышей на плоской пов-сти:
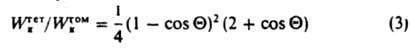
(Q - краевой угол избират. смачивания, отсчитываемый в зародыше; рис. 3). Работа образования критич. зародыша при гетерог. З. н. ф. всегда ниже, чем при гомогенном, и меняется от Wкгом до 0 при изменении Q от 180° до 0°. 3. н. ф. еще более облегчается на дефектах структуры пов-сти - в царапинах, порах и др. С этим, в частности, связано использование пористых "кипятильников" при перегонке.
При гомог. образовании кристаллич. зародышей (при затвердевании, кристаллизации из р-ра) их форма определяется условием Гиббса-Кюри минимума поверхностной энергии зародыша Sgisi, где gi и si - соотв. уд. свободные поверхностные энергии и площади i-х граней кристалла. Этому условию отвечает соотношение Вульфа: gi/hi = const, где hi - расстояние i-й грани от центра кристалла. Зависимость DG(hi) при образовании кристаллич. зародышей сходна с выражением (1), но численные коэф. оказываются иными. Часто выражение (1) применяют и при рассмотрении образования кристаллич. зародышей, подразумевая под величиной g нек-рое усредненное (эффективное) значение уд. поверхностной энергии зародыша. При гетерог. образовании кристаллич. зародышей важное значение имеет структурное соответствие зародыша и матрицы, на к-рой он образуется. Выделение кристаллич. фазы на подложке с близкими параметрами их кристаллич. структуры наз. эпитаксиальным ростом. Как особый вид гетерог. З. н. ф. можно рассматривать возникновение двухмерных зародышей при кристаллизации: новых атомарных (молекулярных) плоскостей с высотой а, равной межплоскостному расстоянию. При этом для зародышей квадратной формы с длиной ребра l:
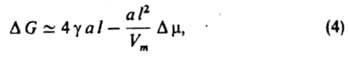
критич. размер зародыша lк = 2gVm/Dm, работа его образования Wк = 4g2аVm/Dm. Возникновение двухмерных зародышей может определять скорость кристаллизации.
При З. н. ф. в кристаллич. фазе необходимо учитывать энергию упругих напряжений, возникающих из-за различия плотностей И. ф. и Н. ф.
В ряде случаев, особенно для высоковязких (напр., полимерных) систем, м. б. достигнута область абс. неустойчивости. При происходящем при этом "спинодальном распаде" З. н. ф. не связано с преодолением энергетич. барьера. 3. н. ф. без преодоления энергетич. барьера возможно и при низких т-рах за счет проявления квантовых эффектов ("квантовое подбарьерное туннелирование").
Кинетическая теория З. н. ф. - сложная проблема, рассмотрению к-рой посвящены работы Я. Б. Зельдовича, Я. И. Френкеля, Р. Беккера, В. Дёринга и мн. др. ученых. Возникновение способного к дальнейшему росту зародыша с размером, большим критического, рассматривается как флуктуационный процесс образования термодинамически невыгодного микросостояния, т. е. состояния, к-рому отвечает увеличение энергии системы.
Если величина Dm мала, в системе возникает равновесное распределение зародышей по размерам, к-рое м. б. описано равновесной ф-цией распределения: f0 (r) = N1ехр(—DG(r)/kT), где k - постоянная Больцмана, N1 - обычно рассматривается как число мест, к-рые может занимать центр зародыша: оно приближенно равно числу молекул в единице объема системы (иногда учитываются нек-рые дополнит. энтропийные эффекты). Поскольку при малых Dm величина Wк = DG(rк) велика, вероятность образования критич. зародышей пренебрежимо мала, а значит невозможно образование и термодинамически выгодных крупных зародышей, для к-рых DG(r) < 0, и ф-ция распределения f0(r) относится только к докритич. зародышам. При достаточно высоком Dm и низком Wк появление критич. зародыша становится достаточно вероятным, а после присоединения к нему одной или неск. молекул его рост становится необратимым. Можно сказать, что в такой системе случайные процессы увеличения и уменьшения размеров зародышей ведут к их направленной "диффузии вдоль оси размеров" к закритич.
состоянию. При этом устанавливается нек-рая стационарная ф-ция распределения зародышей по размерам f(r), отличающаяся от равновесной f0(r). Частота образования закритич. зародышей I (их число, возникающее в единицу времени в единице объема системы) описывается выражением вида:
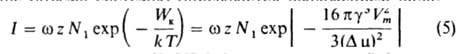
В этом выражении z =f(rк)/f0(rк) - "неравновесный фактор", к-рый, по Зельдовичу, пропорционален (g/kT)1/2. "Кинетич. фактор" w описывает скорость роста критич. зародыша; обратную величину 1/w можно рассматривать как время жизни критич. зародыша, т. е. время присоединения к нему еще одной молекулы, переводящей его в закритич. состояние. Выражения для со сложны и зависят от типа фазового перехода. Так, для случая конденсации пара:
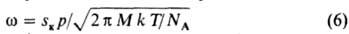
(NA - число Авогадро).
Существенная зависимость частоты образования зародышей (I) от Dm приводит к тому, что гомог. 3. н. ф. возможно только при достаточно высоких значениях Dm, после чего происходит резкий рост I с увеличением Dm. Дальнейший рост сверхкритич. зародышей может определяться скоростью подвода в-ва из объема И. ф., скоростью отвода тепла, выделяющегося при фазовом переходе, или скоростью пристраивания молекул к пов-сти растущего зародыша. Поскольку Dm снижается вблизи растущей частицы, вероятность образования новых зародышей в системе со временем уменьшается. Если скорость образования новых зародышей велика, а скорость их роста мала, образуется высокодисперсная система. Это, в частности, возможно при введении в систему ПАВ (модификаторов первого рода по Ребиндеру), уменьшающих работу образования критич. зародыша вследствие снижения поверхностного натяжения и затрудняющих дальнейший рост частиц в результате адсорбции на их пов-стях. Близкая к монодисперсной система м. б. получена: при длит. поддерживании в системе пересыщения за счет медленно протекающей хим. р-ции образования труднорастворимого в-ва (напр., получение золя серы при сливании разб. р-ров Na2 S2 O3 и серной или соляной к-ты); при введении большого числа зародышей (модификаторов второго рода) - этот метод используется в технологии, напр., ТiO2. При выращивании монокристаллов (напр., для полупроводниковой или лазерной техники) в системе постоянно поддерживают заданное пересыщение и отложение в-ва ведут на затравках. С гетерог. 3. н. ф. на кристалликах соли связано образование облаков.
Дальнейшая эволюция дисперсной системы, образующейся при 3. н. ф., м. б. связана с протеканием процессов коагуляции и переноса в-ва от малых частиц к более крупным (оствальдово созревание). Перенос обусловлен различием хим. потенциала в-ва в частицах разных размеров (эффект Гиббса-Томсона).
При эксперим. исследованиях 3. н. ф. в связи с трудностями измерения I (Dm) часто определяют критич. пересыщение Dmк, соответствующее границе метастабильности, т. е. точке вскипания перегретой жидкости, точке росы пересыщенного пара и т. д. Сложности эксперим. исследования:
1. Малые размеры зародышей, затрудняющие их прямое наблюдение. Поэтому при кристаллизации из расплава пользуются методом "проявления" - И. ф. после выдержки при исследуемом переохлаждении быстро доводят до т-ры "проявления", при к-рой возникшие зародыши дорастают до видимых размеров, а новые не возникают. Делением числа полученных зародышей на время выдержки получают скорость зарождения.
2. Наличие неконтролируемых процессов гетерог. 3. н. ф., что затрудняет реализацию гомог. зарождения, происходящего медленнее. Число посторонних частиц уменьшают тщательной очисткой И. ф. Очень эффективен метод малых капель: при диспергировании образца инородные частицы попадают лишь в нек-рые из капель, вызывая в них гетерог. 3. н. ф. В основной же массе капель зарождение носит гомог.
характер. Статистич. обработка экспериментов с ансамблем капель позволяет найти 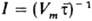 , где Vm - объем капли, , где Vm - объем капли, 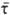 - среднее время ожидания зародыша. Очень высокие значения I ~ 1022 - 1031 м-3 с-1 получены в экспериментах по кристаллизации металлич. пленок, в к-рых отдельные капельки имели размеры 10-9 — 10-8 м.
Исследование 3. н. ф. при конденсации проводится с помощью методики адиабатич. расширения в камере Вильсона и в сверхзвуковых соплах, а также методом стационарного тепло- и массопереноса в диффузионных камерах. - среднее время ожидания зародыша. Очень высокие значения I ~ 1022 - 1031 м-3 с-1 получены в экспериментах по кристаллизации металлич. пленок, в к-рых отдельные капельки имели размеры 10-9 — 10-8 м.
Исследование 3. н. ф. при конденсации проводится с помощью методики адиабатич. расширения в камере Вильсона и в сверхзвуковых соплах, а также методом стационарного тепло- и массопереноса в диффузионных камерах.
===
Исп. литература для статьи «ЗАРОЖДЕНИЕ НОВОЙ ФАЗЫ»: Хирс Д., Паунд Г., Испарение и конденсация, пер. с англ., М., 1966; Френкель Я. И., Кинетическая теория жидкостей, Л., 1975; Лифшиц Е. М., Питаевский Л. П., Физическая кинетика, М., 1979; Методы Монте Карло в статистической физике, пер. с англ., М., 1982; Фольмер М., Кинетика образования новой фазы, пер. с нем., М., 1986; Скрипов В. П., Коверда В. П., Спонтанная кристаллизация переохлажденных жидкостей, М., 1984; Langer J. S., "Annals of Physics", 1969, v. 54, p. 258-72; Nucleation, N.Y., 1969; Nucleation phenomena, Amst., 1977. A. B. Перцов.
Страница «ЗАРОЖДЕНИЕ НОВОЙ ФАЗЫ» подготовлена по материалам химической энциклопедии.
|

