КОЛЕБАТЕЛЬНЫЕ РЕАКЦИИ, р-ции, в ходе к-рых концентрации промежут. соединений и скорость р-ции испытывают колебания. Колебания м. б. периодическими, в этом случае значения c(t) колеблющихся концентраций (t - время) можно представить рядом Фурье:
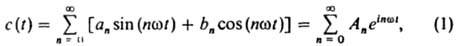
где аn, bn - коэффициенты разложения ф-ции c(t) в рад (амплитуды отдельных гармонич. компонент), An - комплексные амплитуды, w - частота колебаний (i - мнимая единица). В общем случае амплитуды и частоты колебаний могут изменяться во времени (колебания затухающие, нарастающие, модулированные). Колебания концентраций промежут. соед. могут быть непериодическими или иметь непрерывный спектр.
Колебания концентраций промежут. соед. - относительно редкое явление, наблюдаемое в ходе нек-рых сложных р-ций. Элементарные хим. р-ции являются релаксац. процессами, обеспечивающими монотонное приближение реагирующей системы к состоянию термодинамич. равновесия. Для возникновения колебаний в ходе гомог. изотермич. р-ции необходимо наличие промежут. соед. и взаимодействие между ними. В открытых системах существуют стационарные состояния, в к-рых концентрация c(i) i-го промежут. соед. не зависит от времени (сi=c0i). При небольших отклонениях системы от стационарного состояния изменение сi описывается суммой экспонент с комплексными показателями:
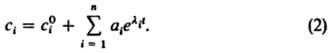
Величины li=gi+iwi, наз. характеристич. числами. В неколебат. устойчивых системах li отрицательны и действительны (gi<0, wi=0). В этих случаях обычно вместо li используют времена релаксации ti=1/li. Если стационарное состояние достаточно близко к состоянию термодинамич. равновесия (выполняются соотношения взаимности Онсагера, см. Термодинамика необратимых процессов), то все li действительны и отрицательны (теорема Пригожина). В этом случае система приближается к стационарному состоянию без колебаний. В сильно неравновесных системах li могут стать комплексными числами, что соответствует появлению колебаний около стационарного состояния. При определенных значениях параметров сильно неравновесной системы (концентраций исходных реагентов, т-ры, давления и т.д.) стационарное состояние может потерять устойчивость. Потеря устойчивости стационарного состояния является частным случаем бифуркации, т.е. изменения при определенном (бифуркационном) значении к.-л. параметра числа или типа разл. кинетич. режимов системы. Имеется два простейших случая бифуркации устойчивого стационарного состояния. В первом случае одно li становится положительным. При этом в точке бифуркации (li=0) исходно устойчивое состояние становится неустойчивым или сливается с неустойчивым стационарным состоянием и исчезает, а система переходит в новое устойчивое состояние. В пространстве параметров в окрестности этой бифуркации существует область, где система обладает по крайней мере тремя стационарными состояниями, из к-рых два устойчивы, а одно неустойчиво. Во втором случае действит. часть одной пары комплексных характеристич. чисел становится положительной. При этом в окрестности потерявшего устойчивость стационарного состояния возникают устойчивые колебания. После прохождения точки бифуркации при дальнейшем изменении параметра количеств, характеристики колебаний (частота, амплитуда и т.д.) могут сильно меняться, но качеств. тип поведения системы сохраняется. В хим. системах неустойчивости могут возникать в результате ускорения р-ции ее продуктами или др. видов автокатализа, субстратного или перекрестного ингибирования (см. Ингибиторы), конкуренции исходных в-в за промежут. соед. и т.п. В неизотермич. системах причиной неустойчивости может служить самоускорение экзотермич. стадий р-ции, а в электрохим. р-циях экспоненциальная зависимость скорости р-ции от поляризации электродов. Появление простейших неустойчивостей и соответствующих кинетич. состояний системы удобно пояснить на примере ферментативной р-ции с двумя
субстратами S1 и S2, один из к-рых, напр. S1, ингибирует фермент Е:
S01DS1 S02DS2 S1+E1 DS1E S1E+S2DS1E:P S1E+S1DS1S1E
Субстраты S1 и S2 могут поступать в систему извне (напр., за счет притока в проточном реакторе или путем диффузии через мембрану) или образовываться в результате медленных гомог. р-ций S0iDSi (i=1,2); так же происходит удаление продукта Р, не влияющего на ход р-ции. S1E, S1S2E и S1S1Е - фермент-субстратные комплексы; ингибирование фермента происходит из-за образования неактивного комплекса S1S1E. В этой системе имеется 6 динамич. переменных: концентрации субстратов [S1] и [S2], фермента [Е] и разл. форм фермент-субстратных комплексов, причем [Е] + [S2E]+[S1S2E]+[S1S1E]=е - полная концентрация фермента. Обычно e<<[S1] и e<<[S2], поэтому можно применить квазистационарности приближение и представить концентрации фермент-субстратных комплексов как алгебраич. ф-ции концентраций субстратов. В результате поведение системы можно описать двумя дифференц. ур-ниями относительно [S1] и [S2]. Удобно использовать безразмерные переменные s1=[Sl]/K1 и s2=[S2]/K2 (K1 и К2 - константы Михаэлиса), параметры a1 и a2 - скорости поступления субстратов, а также безразмерные комбинации констант скорости элементарных стадий e, b, g, d, ( и безразмерное время t. Тогда дифференц. ур-ния принимают вид:
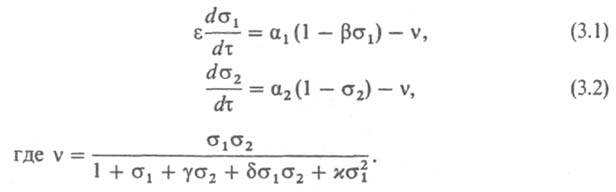
Рассмотрим случай, когда эта система имеет два устойчивых стационарных состояния - бистабильную систему, или триггер. Если a2>>a1/e, т.е. скорость р-ции S02DS2 очень велика по сравнению со скоростью р-ции S01DS1 и скоростью ферментативной р-ции, то [S2] постоянна и равна [S02]. В этом случае поведение системы описывается только одним ур-нием (3.1). Зависимости dsl/dt от s1 при разных значениях a1 показаны на рис. 1, а. Пунктирные кривые соответствуют бифуркац. значениям параметра a-a'1 и a:1, а кривые, заключенные между ними, трижды пересекают ось абсцисс. Точки пересечения соответствуют стационарным состояниям s101, s102 и s103, среднее из к-рых s102 неустойчиво и разделяет области притяжения устойчивых состояний s101
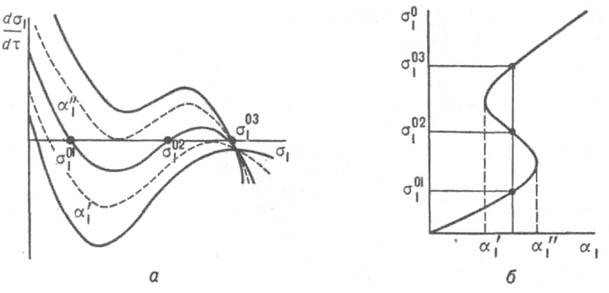
Рис. 1. Ферментативная система с тремя стационарными состояниями (биохим. триггер): a зависимость скорости ds1/dt изменения безразмерной концентрации субстрата S1, от ее значения (s1) при разл. скоростях (a1) поступления субстрата; пунктиром обозначены кривые, соответствующие бифуркац. значениям a'1 и a''1; 6 - зависимость стационарных значений s01 от a1; s101 и s103 устойчивые, s102 - неустойчивое стационарные состояния.
и s103. На кривой зависимости стационарной концентрации s10 от a1 (рис. 1, б) область с тремя стационарными состояниями лежит в интервале (a'1, a''1). При прямом и обратном медленном изменении параметра a1 происходит движение системы по различным траекториям, т.е. гистерезис. Следует отметить, что описанную бистабильность можно получить в системе с односубстратной р-цией, к-рая ведет себя аналогично двухсубстратной р-ции с фиксир. концентрацией одного из субстратов.
Чтобы система с одной переменной и бистабильностью стала колебательной, нужно превратить параметр в медленную переменную. В ферментативной системе с двумя субстратами таким параметром, естественно, является концентрация второго субстрата s2. В этом случае для описания системы нужно использовать оба ур-ния (3). Относительные изменения концентрации S2(D[S2]/[S2]) будут медленными по сравнению с относительными изменениями Sl, если [S2]>>[S1]. При переходе к безразмерным параметрам это условие принимает след, вид: a1~a2~1, e<<1. На фазовой плоскости с координатами s1, s2 поведение системы качественно определяется взаимным расположением нуль-изоклин-кривых, на к-рых производные ds1/dt и ds2/dt равны 0 (рис. 2, а). Точки пересечения нуль-изоклин соответствуют стационарным состояниям системы. Пунктиром показано положение нуль-изоклины ds1/dt=0 при бифуркации, сопровождающейся возникновением устойчивых колебаний (автоколебаний) малой амплитуды. Этим колебаниям соответствует замкнутая траектория движения системы - т. наз. предельный цикл. Сплошными линиями показаны нуль-изоклины в ситуации, далекой от бифуркации, когда единственное стационарное состояние системы (точка О на рис. 2, а) сильно неустойчиво и окружено предельным циклом ABCD. Движению системы по этому предельному циклу соответствуют автоколебания концентраций s1 и s2 с большой амплитудой (см. рис. 2, б).
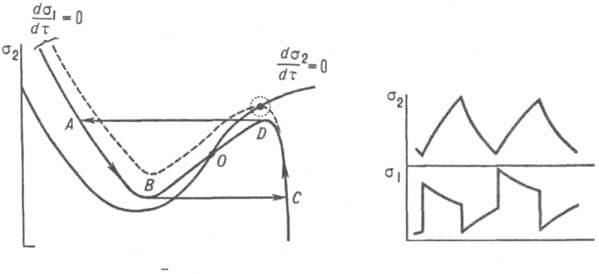
Рис. 2. Автоколебания (устойчивые колебания) в модельной ферментативной системе: a-фазовая плоскость в координатах s1-s2 с нуль-изоклинами ds1/dt=0, ds2/dt=0; пунктиром показано положение нуль-изоклины ds1/dt=0, соответствующее колебат. бифуркации, и малый предельный цикл, окружающий потерявшее устойчивость стационарное состояние О, ABCD большой предельный цикл; б - автоколебания концентраций s1 и s2, соответствующие большому предельному циклу ABCD.
В ходе К. р. наблюдались периодич. колебания разл. формы: синусоидальные, пилообразные, прямоугольные и т.д.; модулированные, квазипериодические и стохастические. Периоды большинства К. р. лежат в диапазоне от долей секунды до десятков минут. К жидкофазным К. р. относятся, напр., диспропорционирование Н2О2 и S2O42-, окисление разл. в-в галогенкислородными соед., окисление углеводородов и сульфидов кислородом. Хорошо изучена Белоусова - Жаботинского реакция, идущая в водном р-ре, где НВrO3 при катализе ионами металлов переменной валентности окисляет разл. орг. соед., в частности малоновую к-ту.
Газофазные К. р. обнаружены и исследованы при окислении паров фосфора, углеводородов, СО и др. соединений. Во всех случаях существенны как объемные стадии р-ции, так и обрыв и зарождение цепей на стенках реактора, а также ускорение р-ций за счет разогрева системы в результате
экзотермич. стадий (тепловой автокатализ). Возможны чисто термокинетич. автоколебания, когда тепловой автокатализ является единств, причиной неустойчивости. Простейшая модель термокинетич. колебаний в проточном реакторе имеет вид: В0:В:Р+Q. Здесь в-во В поступает в проточный реактор идеального смешения, где происходит мономолекулярная экзотермич. р-ция распада; выделяющееся тепло отводится через стенку реактора. Кинетика этой р-ции описывается двумя дифференц. ур-ниями относительно концентрации В и т-ры Т внутри реактора:

где [В0] - приведенная концентрация на входе в реактор, Т0 - т-ра стенки реактора, k - коэф. скорости обновления реакц. смеси в реакторе, h - коэф. скорости теплообмена, Q - тепловой эффект р-ции, Ср - теплоемкость при постоянном давлении, r - плотность, Е и А - энергии активации и предэкспоненциальный множитель р-ции соотв., R - газовая постоянная. В этой системе саморазогрев ускоряет р-цию, что приводит к исчерпанию В в реакторе и замедлению р-ции; затем концентрация В растет вследствие его поступления в реактор и цикл повторяется.
Гетерог. К. р. имеют место при окислении СО, Н2, NH3, С2Н4, СН3ОН на катализаторах платиновой группы. Часто колебания наблюдаются при растворении или осаждении металлов на границе металл - раствор. Обычно эти К. р. связаны с электрохим. р-циями образования новой фазы. На рис. 3, а-е показаны примеры различных
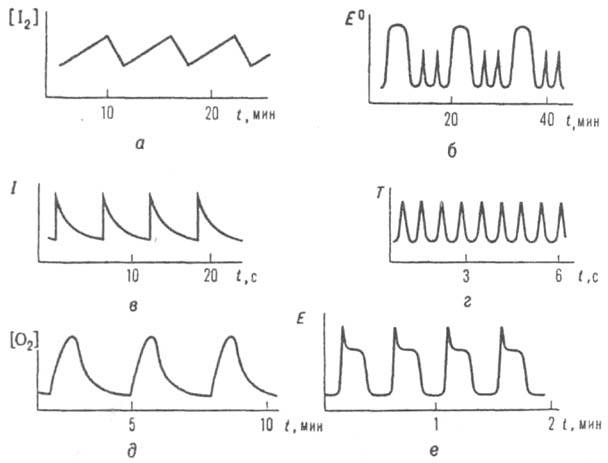
Рис. 3. Автоколебания в разл. хим. системах: а колебания концентрации I2 при разложении Н2О2 в присут. IО3; 6 колебания окислит.-восстановит. потенциала E0 р-ра при окислении S2O32- хлоритом; в колебания интенсивности I хемилюминесценции при газофазном окислении СО; г - колебания т-ры DT0 при газофазном окислении СН3СНО; д - колебания конц. О2 при окислении Н2 на Ni; е - колебания электродного потенциала E при растворении Fe в HNO3.
автоколебат. хим. систем. К. р. может протекать и в распределенной системе, где имеется диффузионная связь между отдельными элементами пространства, напр. при р-циях в тонком слое неперемешиваемой жидкости. В таких случаях возникают бегущие концентрац. волны.
Колебания могут возникать при работе проточных реакторов (напр., при полимеризации этилена, окислении СО). Обычно они вредны, снижают однородность продукта, приводят к аварийным ситуациям. Однако в ряде случаев проведение р-ции в колебат. режиме может быть полезным. Напр., средняя скорость каталитич. окисления SO2 на V2O5 возрастает в колебат. режиме на 15%; в ряде
процессов полимеризации в результате колебаний скорости подачи мономера снижается полидиспeрсность продукта.
К. р. лежат в основе ряда важнейших биол. процессов: генерации биоритмов, мышечного сокращения и т.д. Важнейшая биол. К. р.- генерация нервных импульсов, вызываемая изменением проницаемости трансмембранных ионпроводящих каналов.
Лит.: Жаботинский А. М., Концентрационные автоколебания, М., 1974; Вольтер Б. В., Сальников И. Е., Устойчивость режимов работы химических реакторов, М.. 1981; Полак Л. С., Михайлов А. С.. Самоорганизация в неравновесных физико-химических системах, М., 1983; Гарел Д., Гарел О., Колебательные химические реакции, пер. с англ., М., 1986; Колебания и бегущие волны в химических системах, под ред. Р. Дж. Филда и М. Бергера, пер. с англ., М., 1987. А. М. Жаботинский.
===
Исп. литература для статьи «КОЛЕБАТЕЛЬНЫЕ РЕАКЦИИ»: нет данных
Страница «КОЛЕБАТЕЛЬНЫЕ РЕАКЦИИ» подготовлена по материалам химической энциклопедии.
|

