ПОВЕРХНОСТЬ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ (ППЭ), потенциальная ф-ция (потенциал) взаимодействия атомных ядер в изолир. молекуле или хим. системе, состоящей из взаимодействующих атомов и (или) молекул. Система, содержащая N атомов, в общем случае имеет z — 3N — 6 внутр. степеней свободы q_i (i= 1, 2,..., z), к-рые можно выбирать разл. способами. Потенциал U ядер атомов (т.е. ППЭ) является ф-цией этих степеней свободы: 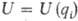. Он входит в ядерное ур-ние движения (эволюции) системы и наряду с оператором кинетич. энергии ядер T составляет ядерный гамильтониан H_яд (см. Квантовая химия):

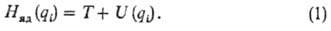
В квантовохим. расчете ППЭ 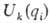для к-го электронного состояния находят решением электронного ур-ния Шрёдин-гера

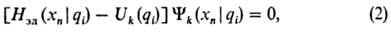
в к-ром электронный гамильтониан H_эл и электронная волновая ф-ция 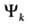зависят от координат электронов x_n (пространственных и спиновых) как от переменных, а координаты ядер являются параметрами. В ур-нии (2) различие между x_n и q_i обозначено вертикальной чертой. Ур-ние (2) решается многократно для разл. совокупностей параметров q_i ,т.е. для разл. фиксир. ядерных конфигураций. Получаемая в результате ППЭ U_k(q_i) наз. электронным термом [обычно если квантовое число k электронного состояния не указано, то назв. "ППЭ" относится к осн. состоянию k = 0, т.е. U(q_i) =U₀(q_i)].

Соотношения (1) и (2) являются мат. выражением адиабатического приближения, в рамках к-рого сначала решается электронное ур-ние (2), а затем найденный электронный терм используется в качестве потенциальной энергии системы в ур-ниях движения с ядерным гамильтонианом (1). T. обр., понятие ППЭ связано с разделением электронного и ядерного движений, к-рое возможно благодаря тому, что в большинстве хим. систем ядерные движения гораздо медленнее электронных. В нек-рых случаях условия разделения электронных и ядерных переменных нарушаются (напр., в области сближения электронных термов) и тогда состояние системы не м. б. охарактеризовано с помощью единственной ППЭ (см. Яна-Теллера эффекты).

Понятие ППЭ применяют во мн. областях теоретич. химии (мол. спектроскопия, безызлучат. квантовые переходы, межмол. взаимодействия, конформац. анализ и др.). Наиб. плодотворно его применение в теории хим. р-ций.

ППЭ представляет собой многомерный геом. объект. Ее осн. элементы-стационарные точки (минимумы и седловые точки), хребты и долины - непосредственно связаны с описанием устойчивых состояний хим. системы и переходов между ними, т.е. хим. р-ций. Топографич. интерпретация очевидна для трехмерной ППЭ, когда U зависит всего от двух координат q₁ и q₂. Ee можно распространить и на многомерные ППЭ. Стационарные точки на ППЭ удовлетворяют ур-ниям:

Матрица вторых производных

в минимумах имеет только положит. собств. значения. В седловых (перевальных) точках она имеет одно отрицат. собств. значение и (z — 1) положительных. Стационарные точки, в к-рых F имеет более одного отрицат. собств. значения, наз. седловыми точками высшего порядка (второго, третьего и т.д.) или, согласно топографич. интерпретации, вершинами.

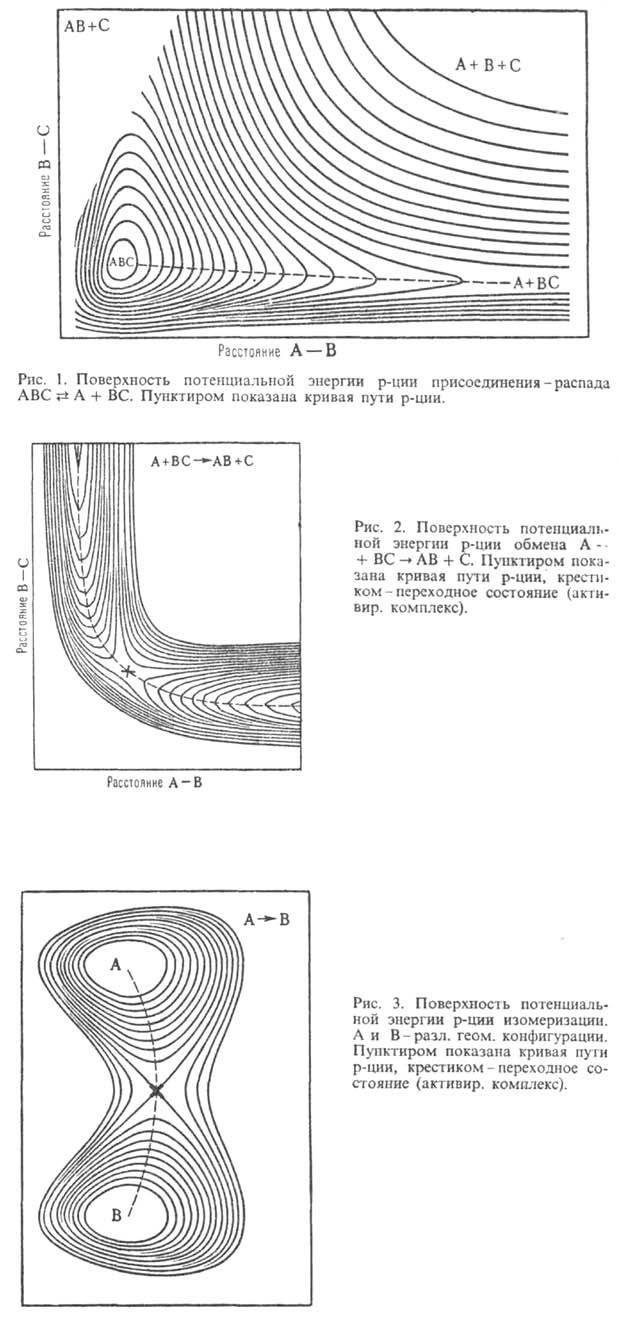
Примеры простых ППЭ приведены на рис. 1-3 как ф-ции двух координат. Они изображены в виде системы энергетич. контуров, т.е. линий, вдоль к-рых потенциальная энергия хим. системы принимает постоянные значения. В трехатомной системе А, В и С разные ППЭ описывают разрыв связи между атомами А и В (рис. 1) и р-цию обмена (рис. 2). Предполагается, что в ходе р-ций все три атома расположены на одной прямой линии и изменение системы полностью описывается двумя межатомными расстояниями. Для р-ции изомеризации (рис. 3) координаты не конкретизированы, А и В означают разл. геом. конфигурации многоатомной системы. Минимумы энергии соответствуют устойчивым ядерным конфигурациям (ABC на рис. 1, ВС и AB на рис. 2), а седловые точки - переходным состояниям (обозначены крестиком на рис. 2 и 3, на рис. 1 ППЭ не имеет седловой точки).

Рис. 1 и 2 иллюстрируют понятие долины на ППЭ. Когда реагируют или образуются в результате р-ции две устойчивые частицы, то на ППЭ имеются области с асимптотич. направлениями, вдоль к-рых частицы сближаются или разлетаются. В отличие от истинных минимумов, асимптотич. область (дно долины) характеризуется одним нулевым собств. значением матрицы F. Соответствующий собств. вектор определяет асимптотич. направление долины. Более сложно определить долину в неасимптотич. области ППЭ, где происходит перестройка хим. связей. Такие участки имеются на ППЭ любых р-ций. Их характерным признаком является то, что (z — 1) независимых энергетич. сечений ППЭ проходят через минимум в точке дна долины. Совокупность таких точек представляет собой кривую в пространстве координат q_i и наз. кривой пути р-ции (см. Координата реакции). На рис. 1-3 координата р-ции показана пунктирной линией. В асимтотич. областях эта кривая становится прямой, т.е. описывает единств. элементарное движение q_i . Аналогично определяются энерге-тич. хребты, разделяющие долины. Гребни хребтов-кривые в пространстве координат q_i вдоль к-рых (z — 1) независимых энергетич. сечений проходят через экстремум, причем по крайней мере один из этих экстремумов-максимум.

Различия ППЭ для трех указанных типов хим. процессов проявляются в их сечениях вдоль координаты р-ции (рис. 4). Для р-ции распада сечение представляет собой кривую с одним минимумом (одноямную кривую) и горизонтальной асимптотич. областью продуктов (рис. 4,а); сплошная кривая соответствует ППЭ без седловой точки (для сравнения см. рис. 1), пунктирная кривая с максимумом отвечает ППЭ р-ции распада с седловой точкой. Для обратной р-ции присоединения в последнем случае имеется потенциальный барьер. Для р-ции обмена сечение ППЭ вдоль координаты р-ции представляет собой кривую с барьером и горизонтальными асимптотич. областями реагентов и продуктов (рис. 4,б), для р-ции изомеризации-двухъямную кривую (рис. 4,в).

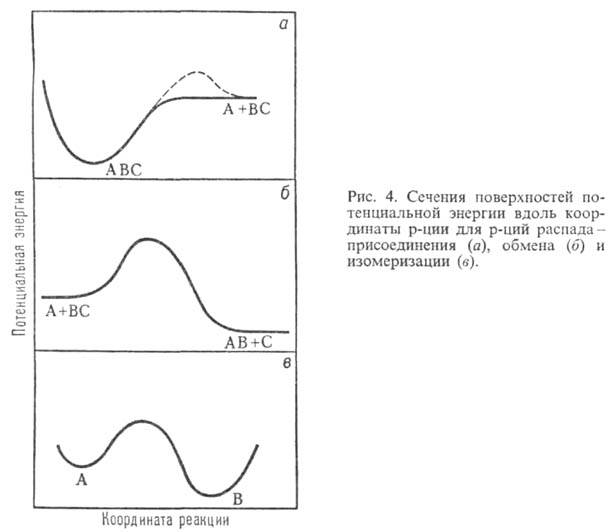
Рис. 5 дает представление о ППЭ сложной р-ции. В системе C₆H₁₀ (число внутр. степеней свободы z = 42) рассматривается р-ция:

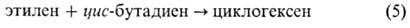
Приведенный малый фрагмент ППЭ системы C₆H₁₀ достаточен для описания процесса (5) и сопутствующего ему конформац. перехода в циклогексене:

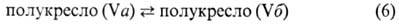
Конфигурации II, IIIa, IIIб соответствуют седловым точкам (переходным состояниям) для согласованного и двух несогласованных механизмов р-ции (5). Конфигурация полуванны IV является переходным состоянием конформац. перехода (6).

Теоретич. исследования хим. р-ций включают три этапа: построение ППЭ, расчет динамики элементарного акта р-ции на этой ППЭ и статистич. усреднение результатов расчета. Итогом вычисления является константа скорости р-ции. Использование активированного комплекса теории позволяет перейти от первого этапа к третьему, минуя динамич. расчет. При этом определение минимумов и сед-ловых точек ППЭ приобретает самостоят. фундам. значение, т. к. нахождение соответствующих геом. конфигураций и их энергий позволяет предсказать. механизм протекания процесса, а после вычисления в этих точках вторых производных [матрицы F (4)] становится доступным расчет константы скорости р-ции. При исследовании динамики (на втором этапе) решаются ур-ния движения с ядерным гамильтонианом (1). В этом случае необходима значительно более подробная информация о ППЭ. Требуется как минимум определить кривую пути р-ции и рельеф ППЭ в ее окрестности.

Прямые вычисления ППЭ стали возможны после разработки эффективных неэмпирич. и полуэмпирич. методов решения электронного ур-ния Шрёдингера (2) для достаточно сложных хим. систем (кон. 60-х гг. 20 в.). Это принципиально важное достижение квантовой химии обусловило последующее бурное развитие теоретич. исследований хим. р-ций. Такие исследования объединяет одна общая особенность: "химически" интересные области ППЭ, прежде всего переходные состояния и нестабильные промежут. соед., определяются с помощью спец. поисковых процедур в кван-товохим. расчете. Напр., схема ППЭ для диенового синтеза (рис. 5) подтверждена серией неэмпирич. и полуэмпирич. вычислений геом. и энергетич. характеристик ее стационарных точек (1970-80).

Надежные квантовохим. расчеты ППЭ для многоатомных систем сложны и дороги. Поэтому пока распространены эмпирич. процедуры построения модельных ППЭ. Они заключаются в выборе эмпирич. ф-ции U(q_i)того вида, к-рый подсказан характером исследуемой р-ции. В ф-цию включаются параметры, подбираемые по эксперим. данным (спектроскопич., термохим., кинетич.) либо оцениваемые в рамках предельно упрощенного теоретич. расчета. Так, в модельных расчетах динамики элементарного акта хим. р-ции часто используют метод Лондона-Эйринга-Поляни-Сато (схема ЛЭПС), а при обсуждении реакционной способности в рамках теории активир. комплекса - метод "порядок связи - энергия связи".

===
Исп. литература для статьи «ПОВЕРХНОСТЬ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ»: Базилевский М.В., Рябой В. M., в сб.: Современные проблемы квантовой химии. Методы квантовой химии в теории межмолекулярных взаимодействий и твердых тел, Л., 1987, с. 3-56. M. В. Базилевский.

Страница «ПОВЕРХНОСТЬ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ» подготовлена по материалам химической энциклопедии.