|
ТУРБУЛЕНТНАЯ ДИФФУЗИЯ,
перенос в-ва в пространстве, обусловленный турбулентным движением среды.
Под турбулентным понимают вихревое движение жидкости или газа, при к-ром элементы
(частицы) среды совершают неупорядоченные, хаотич. движения по сложным траекториям,
а скорость, т-ра, давление и плотность среды испытывают хаотич. флуктуации.
Если в турбулентном потоке
в определенный момент времени множество элементов (частиц) расположено рядом
один с другим, то в послед, моменты времени они рассеиваются по пространству
так, что статистич. расстояние между любыми двумя произвольными частицами с
течением времени возрастает. Проявления этого процесса во многом напоминают
мол. диффузию.
В основе описания T. д.
как процесса случайного блуждания частиц среды лежат выражения для среднеквадратичного
смешения частиц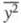 от
нек-рого исходного положения через интервал времени t, сходные с выражениями
для мол. диффузии. В случае больших времен процесса рассеяния, когда м. б. использован
закон Фика, справедливо равенство: от
нек-рого исходного положения через интервал времени t, сходные с выражениями
для мол. диффузии. В случае больших времен процесса рассеяния, когда м. б. использован
закон Фика, справедливо равенство:

где 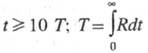 - лагранжев временной масштаб (с) в направлении
переноса; параметр Dt=v2T- коэффициент T. д. (мат. выражение
и физ. смысл см. ниже). Лагранжев коэф. корреляции между пульсациями скорости
v (м/с) одного и того же элемента (частицы) среды в разные моменты времени t
и t +
- лагранжев временной масштаб (с) в направлении
переноса; параметр Dt=v2T- коэффициент T. д. (мат. выражение
и физ. смысл см. ниже). Лагранжев коэф. корреляции между пульсациями скорости
v (м/с) одного и того же элемента (частицы) среды в разные моменты времени t
и t + 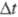 составляет: составляет:
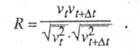
Поскольку T. д. и мол.
диффузия независимы, общее смещение частицы будет определяться суммой:

а общий (виртуальный) коэф.
диффузии Dt = D1. + D, где D -коэф. мол.
диффузии. Хаотич.
пульсац. движение жидкости (газа), обусловливающее турбулентный поток в-ва,
возникает при высоких числах
Рейнольдса (см. Подобия теория). Наличие градиентов осредненной скорости
течения (см. ниже) приводит к заметному ускорению рассеяния частиц в-ва по направлению
турбулентного потока. Его плотность выражают в виде вектора:

где u', с' -
пульсац. составляющие соотв. вектора скорости движения среды и концентрации
переносимого в-ва; < > -оператор осреднения ф-ции по времени в рассматриваемой
точке пространства.
Т.д. протекает по-разному
в зависимости от масштаба турбулентности. Перенос в-ва при маломасштабной турбулентности
описывают по аналогии с мол. диффузией. При крупномасштабной турбулентности
среднее квадратичное смещение частиц с течением времени быстро увеличивается,
причем этот рост обусловлен преим. крупными вихрями.
Предполагают, что турбулентный
перенос в-ва в рассматриваемый момент времени в произвольной точке пространства
определяется градиентом осредненной концентрации, взятым в той же точке пространства
и в тот же момент времени (гипотеза Буссинеска). Так, плотность турбулентного
потока массы в направлении к.-л. из осей координат, напр. *, выражают в виде:

где < с > - средняя
по времени концентрация переносимого в-ва в рассматриваемой точке пространства;
знак "минус" указывает на уменьшение концентрации в направлении
переноса.
Ур-ние (4) служит по существу
определением коэф. пропорциональности Dт. Этот параметр связывает
поток массы при турбулентном режиме течения среды с градиентом осредненной скорости
движения. В настоящее время Dт. не м. б. определен чисто теоретич.
путем.
Используя соотношения,
аналогичные законам вязкости Ньютона и теплопроводности Фурье (см. Переноса
процессы), вводят коэф. турбулентной кинематич. вязкости vт
и турбулентной температуропроводности ат (м2/с). Последние
в отличие от выраженных в тех же единицах измерения коэф. мол. диффузии D, температуропроводности
а и кинематич. вязкости v не являются физ.-хим. характеристиками
и зависят от параметров осредненного движения среды, а также от положения рассматриваемого
элемента ее объема в потоке.
Механизм турбулентного
перемешивания в осн. одинаков для внутр. трения, тепло- и массопроводности.
Различие состоит лишь в особых св-вах переносимой пульсац. течением субстанции:
импульса (кол-ва движения), в-ва или теплоты. Согласно аналогии Рейнольдса,
коэффициенты Т.д., кинематич. вязкости и температуропроводности равны друг другу:
Dт = Vт=ат.. По аналогии с числами Прандтля
(Pr = v/a)и Шмидта
(Sc = v/D) для мол. диффузии вводят понятие о соответствующих коэф.
турбулентного переноса:
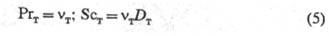
При турбулентном переносе
вблизи твердых пов-стей величины Prт и Scт, на основании
эксперим. данных, несколько отличаются от единицы и обычно находятся в пределах
0,5-1,0. Сказанное свидетельствует о том, что мн. сведения относительно DT
B-B (или ат)в первом приближении можно заимствовать
из имеющейся в справочной литературе информации о Vт.
Турбулентный перенос в-ва
вдали от пов-стей, ограничивающих область движения потока, во много раз превышает
мол. перенос (поэтому перемешивание среды часто осуществляют при турбулентном
режиме течения). Так, для газов коэф. диффузии D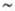 10-5
м2/с, а средний Dт при движении потока, напр, в трубах,
находится в пределах 10-4-10-2 м2/с. Значения
соотношения D/Dт остаются небольшими, напр.: при течении жидкостей
составляют 10-6-10-4. Однако вблизи границы раздела фаз
турбулентность затухает , и мол. диффузия становится преобладающей. 10-5
м2/с, а средний Dт при движении потока, напр, в трубах,
находится в пределах 10-4-10-2 м2/с. Значения
соотношения D/Dт остаются небольшими, напр.: при течении жидкостей
составляют 10-6-10-4. Однако вблизи границы раздела фаз
турбулентность затухает , и мол. диффузия становится преобладающей.
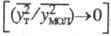
В общем случае выражение
для плотности диффузионного потока в бинарной жидкой или газовой смеси с учетом
мол. и турбулентного механизмов переноса записывают в виде:
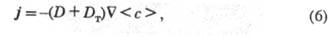
где V - набла-оператор
(Гамильтона оператор).
Знание закономерностей
Т.д. необходимо при описании хим.-технол. процессов, протекающих в потоках жидкости
или газа, в т. ч. в дисперсных средах. T. д. оказывает влияние на структуру
потоков в аппаратах и вносит свой вклад в продольное и поперечное перемешивание
в-ва. Чаще всего продольное перемешивание снижает движущую силу массо-обменных
процессов и ухудшает их показатели.
===
Исп. литература для статьи «ТУРБУЛЕНТНАЯ ДИФФУЗИЯ»: Mонин А. С.,
Яглом А. Я., Статистическая гидромеханика, ч. 1-2, M., 1967; Берд Р., Стыоарт
В., Л айтфут E., Явления переноса, пер. с англ., M., 1974; Рейнольде А.Дж.,
Турбулентные течения в инженерных приложениях, M., 1979. В. В. Дильман.
Страница «ТУРБУЛЕНТНАЯ ДИФФУЗИЯ» подготовлена по материалам химической энциклопедии.
|

