|
ВАРИАЦИОННЫЙ МЕТОД в квантовой химии, метод приближенного решения
ур-ния Шрёдингера для квантовой системы (атома, молекулы, кристалла). По
своей идее близок к мат. методу оценки нек-рой величины из условия максимума
или минимума определенной ф-ции (напр., методу наименьших квадратов).
В квантовохим. задачах В. м. обычно определяют волновую ф-цию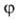 стационарного состояния системы с гамильтонианом Я из условия минимума
среднего значения энергии системы
стационарного состояния системы с гамильтонианом Я из условия минимума
среднего значения энергии системы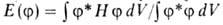 (
(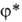 -ф-ция, комплексно
сопряженная с ср; интегрирование проводится по всей области изменения независимых
переменных, описывающих систему). Величина -ф-ция, комплексно
сопряженная с ср; интегрирование проводится по всей области изменения независимых
переменных, описывающих систему). Величина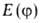 наз. функционалом энергии системы. Согласно т. наз. вариационному принципу,
для любой волновой ф-ции выполняется соотношение:
наз. функционалом энергии системы. Согласно т. наз. вариационному принципу,
для любой волновой ф-ции выполняется соотношение: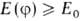 ,
где Еo- наименьшая энергия системы в стационарном состоянии,
т.е. энергия ее осн. состояния. Реально функционал энергии минимизируют
в нек-ром ограниченном классе волновых ф-ций, наз. пробными, к-рые выбирают
на основе физ. представлений о характере взаимод. частиц в системе. Поэтому
если точное решение ур-ния Шрёдингера получить невозможно, то минимизируя ,
где Еo- наименьшая энергия системы в стационарном состоянии,
т.е. энергия ее осн. состояния. Реально функционал энергии минимизируют
в нек-ром ограниченном классе волновых ф-ций, наз. пробными, к-рые выбирают
на основе физ. представлений о характере взаимод. частиц в системе. Поэтому
если точное решение ур-ния Шрёдингера получить невозможно, то минимизируя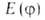 в классе пробных ф-ций, находят волновую ф-цию, к-рая является макс. приближением
к точной волновой ф-ции осн. состояния системы, и приближенное значение
Eo.
в классе пробных ф-ций, находят волновую ф-цию, к-рая является макс. приближением
к точной волновой ф-ции осн. состояния системы, и приближенное значение
Eo.
Нахождение минимума этой ф-ции математически выражается условием обращения
в нуль вариации:
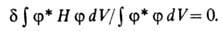
В линейном В.м. (методе Ритца) в кач-ве пробной волновой ф-ции для исследуемой
системы принимают линейную комбинацию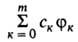 нек-рых разумно выбранных волновых ф-ций
нек-рых разумно выбранных волновых ф-ций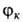 .
При описании молекулярной системы в качестве .
При описании молекулярной системы в качестве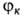 м. 6. выбраны волновые ф-ции, отвечающие разл. валентным схемам (см. Валентных
связей метод), или
м. 6. выбраны волновые ф-ции, отвечающие разл. валентным схемам (см. Валентных
связей метод), или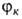 могут описывать отдельные электронные конфигурации системы (см. Молекулярных
орбиталей методы). Коэф. ск линейной комбинации рассматриваются
как переменные параметры системы, функционал энергии - как обычная ф-ция
этих параметров. Приближенное решение ур-ния Шрёдингера проводится в итоге
по след. схеме: 1) рассчитывают матричные элементы гамильтониана Hкl
=
могут описывать отдельные электронные конфигурации системы (см. Молекулярных
орбиталей методы). Коэф. ск линейной комбинации рассматриваются
как переменные параметры системы, функционал энергии - как обычная ф-ция
этих параметров. Приближенное решение ур-ния Шрёдингера проводится в итоге
по след. схеме: 1) рассчитывают матричные элементы гамильтониана Hкl
=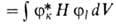 и интегралы
перекрывания и интегралы
перекрывания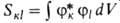 для всех пар ф-ций
для всех пар ф-ций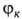 и
и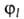 и строят
матрицы гамильтониана Н и перекрывания S. 2) С помощью этих
матриц условие экстремума функционала энергии представляют в форме: и строят
матрицы гамильтониана Н и перекрывания S. 2) С помощью этих
матриц условие экстремума функционала энергии представляют в форме: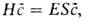 где
где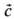 -вектор,
координаты к-рого - ск. 3) Находят ненулевые решения этого ур-ния,
к-рым отвечает т. наз. вековое уравнение (термин небесной механики) det
(Н — — ES) = О (det-символ определителя матрицы). Вековое ур-ние
имеет (m+1) решений -вектор,
координаты к-рого - ск. 3) Находят ненулевые решения этого ур-ния,
к-рым отвечает т. наз. вековое уравнение (термин небесной механики) det
(Н — — ES) = О (det-символ определителя матрицы). Вековое ур-ние
имеет (m+1) решений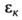 (к = 0, 1, 2, ..., т), к-рые являются оценками сверху для точных значений
энергии системы в стационарном состоянии, занумерованных в порядке их возрастания:
(к = 0, 1, 2, ..., т), к-рые являются оценками сверху для точных значений
энергии системы в стационарном состоянии, занумерованных в порядке их возрастания: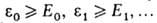 Возможность получения этих значений энергии в рамках линейного В.м. широко
используют для изучения возбужденных состояний молекулярных систем.
Возможность получения этих значений энергии в рамках линейного В.м. широко
используют для изучения возбужденных состояний молекулярных систем.
Применяют и более сложные варианты В.м. Напр., при исследовании молекулы
пробную волновую ф-цию конструируют из орбиталей, характеризующих состояние
электрона в молекуле. Это позволяет найти ур-ния, задающие оптимальный
набор орбиталей и эффективный потенциал, определяющий состояние электронов
в молекуле. В.м. используют также для решения задач теории рассеяния, оценки
энергий возбуждения и ионизации и др. Условие надежности расчетов, получаемых
В. м., - правильные качеств. представления о природе исследуемого объекта
и физически обоснованный выбор класса пробных ф-ций.
===
Исп. литература для статьи «ВАРИАЦИОННЫЙ МЕТОД»: Эпштейн С., Вариационный метод в квантовой химии, пер.
с англ., М., 1977. В. И. Пупышев.
Страница «ВАРИАЦИОННЫЙ МЕТОД» подготовлена по материалам химической энциклопедии.
|

